Fibonacci Numbers in Underwater Photography
What makes an image a really good one is certainly a question, that, at some point, troubles the mind of every image maker. Is it about the subject, or is it about that specific moment captured? Is it about color, or about techniques used? Each of the mentioned aspects deserves consideration, and not every breathtaking image can be entirely explained by just following a checklist, marking the things that were done correctly with a green pen and using a red pen for the failures spotted. Yet, what most humans perceive as beautiful and aesthetically pleasing visually can surprisingly often be explained with math. Yes, math.
Tags & Taxonomy
It is not a new thing. It all began in Pisa, 817 years ago, when a very clever mathematician was thinking profoundly about numbers… and also about rabbits. His name was Leonardo Pisano Bigollo, better known as Fibonacci.
Fibonacci lived around 1170-1250 B.C. and was known to be the most talented mathematician of the Western world in the Middle Ages. As a member of an important trading family in Pisa, he travelled extensively throughout the Middle East as a youth and discovered the mathematical advantages of the Indian number system, which made its way to the West through the Arabic countries. In his time, the Roman numeric system was the one used in Europe, making advanced mathematics difficult, if not impossible.
In Fibonacci's own words (from his book Liber Abaci, published in 1202): “…when I had been introduced to the art of the Indians' nine symbols through remarkable teaching, knowledge of the art very soon pleased me above all else and I came to understand it, for whatever was studied by the art in Egypt, Syria, Greece, Sicily and Provence, in all its various forms.“
Just imagine the year we are living in—2019—in Roman numerals. In Fibonacci's time, this number was written MMXIX. Tricky to do math with that.
A legendary formula
Around the year 1210, Fibonacci returned to Pisa, where he wrote several important texts and books. Copies of his works were extremely limited, as the great mathematician lived 200 years before print was even invented, so his texts and books were handwritten. One of his most well-known books survived the centuries: Liber Abaci (The Book of Calculation). This book introduced the Hindu-Arabic decimal system and the use of Arabic numerals to Europe, an often forgotten but important fact. Forgotten perhaps because what is most often discussed is the problem about rabbits and the legendary mathematical formula resulting from it.
In his work, Fibonacci posed the following question: “A certain man puts a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?” (Fibonacci, Liber Abaci, third chapter)
The resulting sequence, in which each number is the sum of the two preceding numbers, goes like this: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
Behold, the world-renowned Fibonacci sequence, also known as the Fibonacci numbers. Please be patient, I will tell you in a short while what all this has to do with underwater photography.
An amazing proportion
Now Fibonacci himself actually had very practical matters and questions in mind when he studied and researched the deeper meanings of mathematics. Just take economy, accounting and population growth (rabbits!) as examples. Unbeknownst to Fibonacci at the time was that his sequence, or better to yet, the quotient of the adjacent terms, led to an amazing proportion—a proportion that can be found in tiny atoms, in DNA and in hurricanes, in small and large objects everywhere in nature, and even in distant galaxies.
This proportion is known by many names: the golden ratio, the golden mean, phi and the divine proportion, among others. Some even call it nature's secret code. It is a number that translates into a ratio, a ratio that defines beauty and aesthetics in nature and in the arts. The answer to the big question about (the meaning of) the universe, life and all the rest is not “42,” it is 1.618. Nature's secret code—and yes, it is everywhere.
Do you like honey bees? If you divide the female bees by the male bees in any given hive, you will get 1.618. How about sunflowers? Sunflowers, which have opposing spirals of seeds, have a 1.618 ratio between the diameters of each rotation. Neither bees nor sunflowers in sight? Try measuring from your shoulder to your fingertips, and then divide this number by the length from your elbow to your fingertips. Your result will be 1.618. Too difficult? Take the length of your leg and compare it to the length of your arm. This proportion should be near 1.68 in almost all cases. The golden ratio cannot be avoided.
Everything beautiful in nature (including beautiful humans) is based on the golden ratio. Or, as the German philosopher Carl Friedrich von Weizsäcker nailed it down when he said, “Perhaps the omnipresent hidden mathematics of nature is the ground of all beauty.”
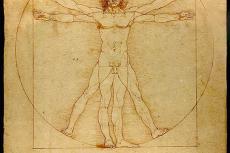
With nature as the greatest teacher, many artists used the golden ratio to create artworks that will stay beautiful forever. Just take Raffael, Leonardo da Vinci, Dali, Rembrandt and Albrecht Dürer as a few examples. In the world of architecture, the Pyramid of Cheops (Giza) in Egypt, the Parthenon in Greece, St. Peter’s Basilica in Italy or Cologne Cathedral in Germany are perfect examples, utilizing the golden ratio, the divine number, the sacred ratio 1.618.
In the underwater world
Once we open our eyes and minds to it, we can spot this divine ratio everywhere, even in the oceans. Seashells, nautilus, crinoids or even corals—everything we perceive as beautiful is based, in one way or another, on the Fibonacci sequence.
For photographers, this leads us to three options (assuming we want to create beautiful images with the divine number in mind): 1) We look out for marine life and subjects that fit into the golden ratio; 2) we compose our images according to the golden ratio; or 3) we combine the first two options above.
Well, not everyone likes math, and we are, at any rate, already overtasked with our diving, traveling, photo gear, and a million other things we need to keep in mind. So, let's start with something easy in terms of how to make use of the “magic number.”
A very basic first step
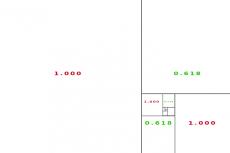
Imagine your picture frame in your camera's viewfinder, LCD screen or on your computer screen in post-production. Divide this frame into two sections. Naturally, you might want to have two sections of the same size. But please don't... as it is not very Fibonacci!
If you want to utilize the golden ratio, the two sections of your picture frame should not be of equal size. To do it “Fibonacci-style”: Create one section that covers roughly 61.8 percent, and another one that covers roughly 38.2 percent of the frame.
To separate the frame into two sections of equal size would mean you subdivide your frame at “50,” or directly down the middle. This could come with the risk of creating a boring image composition.
This works, by the way, with vertical and horizontal subdivisions alike. It also works with all kinds of different image aspect ratios (such as 4:3, 3:2, 1:1 and so on). What is important are the proportions of the sections (please see the image graphic).
Please note that the Fibonacci sequence and its effects on image composition is not the “rule of thirds” and should not be mistaken for it. Image composition using the Fibonacci sequence is a far more advanced thing than the rule of thirds.
After that nice and smooth warm-up, let us proceed with the next step. It is called the phi grid, and again, it is a part of the Fibonacci numbers family.
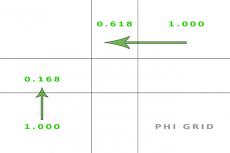
Phi grid
Now, everyone knows the rule of thirds. It divides a frame into three rows and three columns of equal size, resulting in a 1:1:1 ratio vertically and a 1:1:1 ratio horizontally—a well-known basis of image composition. The phi grid, however, works slightly differently. It divides the frame in a similar way as the rule of thirds does but makes the middle row and middle column smaller according to the golden ratio. This results in a 1:1.618:1 ratio vertically and a 1:1.618:1 ratio horizontally. Simply put, the phi grid gives more weight to the top left and right sections, and to the bottom left and right sections of the frame (please see image graphic).
Golden rectangle
Whilst the first example was simple, because we divided a frame into only two sections; and the second example might have been easy to digest as well, since it reminded us somewhat of the rule of thirds; we will now go a little bit deeper into complexity with a third example.
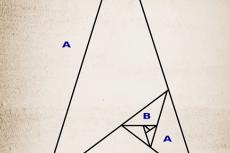
Following the Fibonacci sequence, an image frame can be subdivided into several sections of different dimensions, with each section and the sum of all of them fitting into the 1.618 ratio. Just remember the rabbits!
First, we divide the frame as in the first example, vertically dividing the frame into two sections, utilizing the 1.618 ratio. The larger section, we leave as it is; the smaller one, we divide into two sections horizontally, again in the 1.618 ratio.
The upper one stays as it is; the lower one we again divide horizontally into two sections. Again, we leave one of those new sections as it is and divide the next one. Logically, our sections are getting smaller and smaller. In the end, we have nine squares (outer frame border included) and a perfect Fibonacci sequence. Voila, the “golden rectangle.”
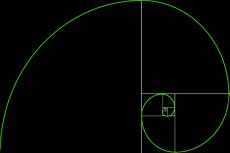
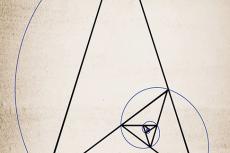
Golden spiral
This one is easy. Take the example above (our collection of different squares) and connect the vertices of these squares with a curved line. Result: The points of these vertices creates a (logarithmic) spiral. Voila, the “golden spiral”—Mother Nature's code of beauty.
The golden spiral is, one could say, a logical result of the Fibonacci sequence. And yes, it is everywhere.
Golden triangle
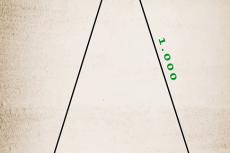
What works with squares works with triangles as well. The “golden triangle” is an isosceles triangle with a vertex angle of 36 degrees and base angles of 72 degrees. The legs are in a golden ratio (1.618 proportion) with the base. A pentagram, for instance, is a perfect example of a combination of golden triangles.
Such a triangle can then be divided into smaller sections, with each section having a “golden number relation” to its neighbor. Connect the vertices of these squares in a curved line and you will have another golden spiral.
Any square-shaped image can be divided into golden triangles to help image composition. Just imagine (or draw) a horizontal line from one corner of the frame to the next. Consider this line to have the value of 1.618. Find a starting point (in your line) that is more or less equal to 1.000 (or at 68.2 percent of the line). From this point, draw another line that ends up in one of the two remaining empty frame corners. You do not have to, but you could draw a last line, starting at 0.618 (or roughly 32.8 percent) of your “main” line, and reaching the last remaining corner of the image frame.
If the composition works according to the Fibonnaci numbers, your main subjects will be oriented to the line(s) and/or fit nicely into the golden triangle sections, which your lines create in the image.
Software
In case you find all this far too complicated to do, you can use Adobe Lightroom or Adobe Photoshop (version CC or later). Both provide the option to adjust or crop your image, utilizing the golden ratio. That does not mean you must crop, but it is a useful visual tool to find out if your image matches the golden ratio or not.
In Adobe Lightroom: When you are using the crop tool, you can cycle through the different options/grids by pressing O (for overlay). You cannot see or access this option unless you are actually using the crop tool. Which overlays (help grids) Adobe Lightroom makes available for you is something you can select by entering: Crop Guide Overlay > Choose Overlays to Cycle.
In Adobe Photoshop: First, the crop tool must be activated. To cycle through the different crop overlays/grids (including the golden ratio, of course), you can use the same keyboard shortcut (O).
Plan B: Just do a search online for “Fibonacci overlays,” and you will find various websites of which some do offer free downloadable overlays with plenty of different golden ratio variations. For example: http://parksphotos.com/goldenoverlays/
These tools are very useful when you want to check if your images are already proud members of the golden ratio or golden number family, or perhaps could use a slight correction to improve their composition. After a little practise, you will easily memorize Mother Nature's special code as it has always been with you… even in your very own DNA.
Composition
However, utilizing the Fibonacci numbers in underwater photography in terms of image composition might not always be easy if one thinks too much about ratios, numbers and math (especially while diving). But then again, many camera user manuals are actually more complicated than the Fibonacci sequence ever was, at least in terms of photography.
Going back to the question posed at the beginning of this article, which was: “What makes an image a really good one?” Perhaps, when selecting your images for a magazine, a contest, an exhibition or just for yourself, have a little dialogue with yourself: “This is so beautiful. I like it! But why is it beautiful? Is it the subject, the light, the colors or something else?”
It could be that the answer to your questions is 1.618, nature's divine code of beauty, the Fibonacci code. This has nothing to do with the camera model used or specific photography techniques applied (not that they are useless, but they are not everything); it has a lot to do with an understanding of what defines beauty. The knowledge of this will certainly help you on your way as a photographer, as it will give you the power to be able to explain why your images are good (beyond subject and technique) and beautiful.
Beauty
Beauty is a universal language. Wise philosophers and scientists in Greece, Egypt and India pondered and studied the “key of beauty” long before Fibonacci was even born. But it was Fibonacci who, by using maths as a universal language, paved a way for making some mysteries of life and nature understandable to humankind.
He did it at a time when the Fourth and Fifth Crusades took place, the Mongolian Gengis Khan ruled an empire and invaded China, truth (what is right and what is wrong) was dictated by religion, and everyone on the planet believed without a doubt that Earth was a disc and the center of the universe. ■
Are you a Fibonacci fan? Learn more about the Fibonacci number sequence and related mathematical topics in The Fibonacci Quarterly (fq.math.ca), a journal published four times a year since 1963, by the Fibonacci Association.
Rico Besserdich is a widely published German photographer, journalist and artist based in Turkey. For more information, visit: Maviphoto.com. See his latest book at: Songofsilence.com.
SOURCES:
Alfred, B. U. (1965). An Introduction to Fibonacci Discovery. Fibonacci Association.
history.mcs.st-andrews.ac.uk
investopedia.com
livescience.com
math.temple.edu
scientificmind.com.np
Download the full article ⬇︎